Interior Angles of a Triangle:
The three interior angles of any triangle add up to 180 degrees
Example: In triangle XYZ, angle Y is twice angle X and angle Z is 40 degrees more than angle Y. How many degrees are in the three angles?
The three angles must total 180 degrees.
Let x = angle X, 2x = angle Y, and 2x + 40 = angle Z:
x + 2x + (2x + 40) = 180.
Angle X = 28 degrees Angle Y = 56 degrees Angle Z = 96 degrees
Similar Triangles
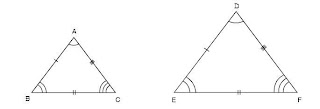
Similar triangles have the same shape;
Two triangles are similar if
(i) their corresponding angles are equal, and
(ii) their corresponding sides are proportional
If ΔABC ~ ΔDEF, then by definition
∠A = ∠D, ∠B = ∠E, ∠D = ∠F and AB/DE=BC/EF=CA/FD
AAA similarity-If in two triangles, the corresponding angles are equal the triangles are similar.
SSS similarity-If the corresponding sides of two triangles are proportional the triangles are
similar.
SAS similarity-If one angle of a triangle is equal to one angle of the other triangle and the sides
containing these angles are proportional, the triangles are similar.
Area of Triangle
Area of Triangle = 1/2 (Base) (Height)
The height is the perpendicular distance between the side that is chosen as the base and the opposite vertex.
Triangle Inequality Theorem
The length of one side of a triangle must be greater than the difference and less than the sum of the lengths of the other two sides.
BASIC PROPORTIONALITY THEOREM
If a line is drawn parallel to one side of a triangle, the other two sides of the triangle are divided proportionally.
If a line divides any two sides of a triangle in the same ratio, the line is parallel
to third side of the triangle.
BISECTOR OF AN ANGLE
The internal bisector of an angle of a triangle divides the opposite side in the ratio of sides containing the angle.
IMPORTANT RESULTS
If a perpendicular is drawn from the vertex of the right angle of a right triangle
to the hypotenuse, the triangles on each side of the perpendicular are similar to
each other and to the triangle.
The ratio of the areas of similar triangles is equal to the ratio of the squares on
their corresponding sides.
