Saturday, November 28, 2009
Friday, November 27, 2009
Thursday, November 26, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 30
Data Interpretation
Data Interpretation involves scientific methods for organizing, summarizing and analyzing data as well as drawing valid conclusion and making reasonable decisions on the basis of such analysis.
Data Interpretation is based on some information (data) from which new information can be deduced. For this section test you need to read quickly and correctly the data represented by various kinds of Graphs, charts, Tables etc.
The data is usually presented first and then some questions are given which are to be answered by drawing inference from the given data. Usually the data pertaining to any situation can be presented in one or more of the following ways.
1. Numerical Data Tables
2. Bar Diagrams
3. Pie-Charts
4. Cartesian graphs
Sentence correction :
Here are some types of errors which you should look for sentence correction.
Misplaced modifiers
Parallel sentences
Pronoun-subject agreement
Proper use of adverbs (they modify verbs)
Proper use of the semicolon
Sentence fragments
Subject-verb agreement
Verb tenses
'Who' versus 'whom'
'Among' versus 'between'
'Fewer' versus 'less'
Prometric has created a CAT 2009 Practical Guide. Please check out the following video...
http://www.youtube.com/watch?v=zaKHWpiFToE
Data Interpretation involves scientific methods for organizing, summarizing and analyzing data as well as drawing valid conclusion and making reasonable decisions on the basis of such analysis.
Data Interpretation is based on some information (data) from which new information can be deduced. For this section test you need to read quickly and correctly the data represented by various kinds of Graphs, charts, Tables etc.
The data is usually presented first and then some questions are given which are to be answered by drawing inference from the given data. Usually the data pertaining to any situation can be presented in one or more of the following ways.
1. Numerical Data Tables
2. Bar Diagrams
3. Pie-Charts
4. Cartesian graphs
Sentence correction :
Here are some types of errors which you should look for sentence correction.
Prometric has created a CAT 2009 Practical Guide. Please check out the following video...
http://www.youtube.com/watch?v=zaKHWpiFToE
Wednesday, November 25, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 29
SET THEORY:
A set is a collection of things.
Each entry in a set is known as an element.
A union of two or more sets is another set that contains everything contained in the previous sets.
Union is designated by the symbol U.
If A and B are sets then A U B represents the union of A and B
The intersection of two (or more) sets is those elements that they have in common.
Intersection is designated by the symbol ∩.
So if A and B are sets then the intersection (the elements they both have in common) is denoted by A∩B.
PROBABILITY:
Probability is a measure of how likely is an event to happen.
It is measured in fractions from 0 to 1 (0 is impossible, 1 is unavoidable or certain).
Sometimes it is denoted in percentages, again from 0% to 100%.
Event is anything that happens. In probability theory we speak of events having outcomes or results.
Example flipping a coin (an event) has two possible outcomes—heads and tails.
When a coin is flipped (an event is tested), one of the outcomes is obtained.
If you know that the probability of an event (or one of the outcomes) is p, the probability of this event NOT happening (or the probability of it NOT having this given outcome), is (1-p).
p(not A) + p(A) = 1
If two (or more) independent events are occurring, and you know the probability of each, the probability of BOTH (or ALL) of them occurring together (event A and event B and event C etc) is a multiplication of their probabilities.
p(A and B) = p(A) * p(B)
p(A and B and C ... and Z) = p(A) * p(B) * p(C) * ... * p(Z)
If two (or more) incompatible events are occurring, the probability of EITHER of them occurring (event A or event B or event C etc) is a sum of their probabilities.
p(A or B) = p(A) + p(B)
p(A or B or C ... or Z) = p(A) + p(B) + ... + p(Z)
Incompatible means that they can't happen together, i.e. p(A and B) = 0. In case of two compatible events, the OR tool looks a bit more complicated:
p(A or B) = p(A) + p(B) - p(A and B)
If we know that A and B are independent, we can apply AND tool to rewrite:
p(A or B) = p(A) + p(B) - p(A) * p(B)
Conditional probability is the probability of some event A, given the occurrence of some other event B. Conditional probability is written P(A|B), and is read "the probability of A, given B". It is defined by
P(A|B)=P(A∩B)/P(B)
A set is a collection of things.
Each entry in a set is known as an element.
A union of two or more sets is another set that contains everything contained in the previous sets.
Union is designated by the symbol U.
If A and B are sets then A U B represents the union of A and B
The intersection of two (or more) sets is those elements that they have in common.
Intersection is designated by the symbol ∩.
So if A and B are sets then the intersection (the elements they both have in common) is denoted by A∩B.
PROBABILITY:
Probability is a measure of how likely is an event to happen.
It is measured in fractions from 0 to 1 (0 is impossible, 1 is unavoidable or certain).
Sometimes it is denoted in percentages, again from 0% to 100%.
Event is anything that happens. In probability theory we speak of events having outcomes or results.
Example flipping a coin (an event) has two possible outcomes—heads and tails.
When a coin is flipped (an event is tested), one of the outcomes is obtained.
If you know that the probability of an event (or one of the outcomes) is p, the probability of this event NOT happening (or the probability of it NOT having this given outcome), is (1-p).
p(not A) + p(A) = 1
If two (or more) independent events are occurring, and you know the probability of each, the probability of BOTH (or ALL) of them occurring together (event A and event B and event C etc) is a multiplication of their probabilities.
p(A and B) = p(A) * p(B)
p(A and B and C ... and Z) = p(A) * p(B) * p(C) * ... * p(Z)
If two (or more) incompatible events are occurring, the probability of EITHER of them occurring (event A or event B or event C etc) is a sum of their probabilities.
p(A or B) = p(A) + p(B)
p(A or B or C ... or Z) = p(A) + p(B) + ... + p(Z)
Incompatible means that they can't happen together, i.e. p(A and B) = 0. In case of two compatible events, the OR tool looks a bit more complicated:
p(A or B) = p(A) + p(B) - p(A and B)
If we know that A and B are independent, we can apply AND tool to rewrite:
p(A or B) = p(A) + p(B) - p(A) * p(B)
Conditional probability is the probability of some event A, given the occurrence of some other event B. Conditional probability is written P(A|B), and is read "the probability of A, given B". It is defined by
P(A|B)=P(A∩B)/P(B)
Tuesday, November 24, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 28
PERMUTATIONS & COMBINATIONS
COMBINATIONS
Number of selections of n different objects taken ‘r‘ at a time.
If the order doesn't matter, it is a Combination.
Number of combinations of n dissimilar things taken 'r' at a time is denoted by nCr & is given by nCr =n!/(n-r)!r!
Number of combinations of n different things taken ‘r’ at a time in which ‘p’ particular things will always occur is (n–p)C(r–p)
Number of combinations of n dissimilar things taken 'r' at a time in which 'p' particular things will never occur is (n–p)Cr

PERMUTATIONS
Number of arrangements of n different objects taken ‘r’ at a time.
If the order does matter it is a Permutation.
A Permutation is an ordered Combination.
Permutations of n different things taken 'r' at a time is denoted by nPr
The total number of arrangements of n things taken ‘r’ at a time, in which a particular thing always occurs = (n–1)P(r–1).
The total number of permutations of n different things taken ‘r’ at a time in which a particular thing never occurs = (n–1)Pr.
The number of arrangements when p of them are of one kind, q of another kind, r is still of another kind and so on, the total number of permutations is given by
n!/(p! q! r !.......)
Number of circular permutations of n things all taken at a time = (n – 1)!
Number of circular permutations of n different things taking ‘r’ at a time =nPr/r
Other Results:
nC0=1
nCn=1
nCr=nCn-r
nCr+nC(r-1)=(n+1)Cr
COMBINATIONS
Number of selections of n different objects taken ‘r‘ at a time.
If the order doesn't matter, it is a Combination.
Number of combinations of n dissimilar things taken 'r' at a time is denoted by nCr & is given by nCr =n!/(n-r)!r!
Number of combinations of n different things taken ‘r’ at a time in which ‘p’ particular things will always occur is (n–p)C(r–p)
Number of combinations of n dissimilar things taken 'r' at a time in which 'p' particular things will never occur is (n–p)Cr

PERMUTATIONS
Number of arrangements of n different objects taken ‘r’ at a time.
If the order does matter it is a Permutation.
A Permutation is an ordered Combination.
Permutations of n different things taken 'r' at a time is denoted by nPr
The total number of arrangements of n things taken ‘r’ at a time, in which a particular thing always occurs = (n–1)P(r–1).
The total number of permutations of n different things taken ‘r’ at a time in which a particular thing never occurs = (n–1)Pr.
The number of arrangements when p of them are of one kind, q of another kind, r is still of another kind and so on, the total number of permutations is given by
n!/(p! q! r !.......)
Number of circular permutations of n things all taken at a time = (n – 1)!
Number of circular permutations of n different things taking ‘r’ at a time =nPr/r
Other Results:
nC0=1
nCn=1
nCr=nCn-r
nCr+nC(r-1)=(n+1)Cr
Sunday, November 22, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 27
Cuboid:
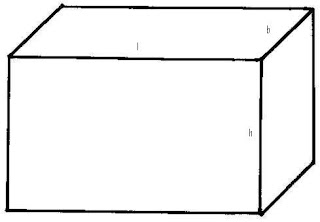
Lateral surface area -- 2h (l + b)
Total surface Area -- 2(lb + bh + lh)
Volume -- lbh
Where
l = length
b = breath
h = height
Cube:

Lateral surface area -- 4a*a
Total surface Area -- 6a*a
Volume -- a*a*a
Where
a = length of edge
Right circular cylinder:

Lateral surface area -- 2πrh
Total surface Area -- 2πr(r + h)
Volume -- π*r*r*h
Where
r = radius of base
h = height of the cylinder
Right circular cone:

Lateral surface area -- πr l
Total surface Area -- πr(l + r)
Volume -- (1/3)π*r*r*h
Where
h = height
r = radius
l = slant height
Sphere:

Total surface Area -- 4πr2
Volume -- (4/3)π*r*r*r
Where
r = radius
Hemisphere:

Lateral surface area -- 2πr*r
Total surface Area -- 3πr*r
Volume -- (2/3)π*r*r*r
Where
r = radius
Spherical shell:

Total surface Area -- 4π (R*R – r*r)
Volume -- (4/3)π(R*R*R -r*r*r)
Where
R = outer radius
r = inner radius
Volume of bucket:

Total surface Area -- πr(l + (R-r))
Volume -- (πh/3)(R*R- r*r)
Where
R = larger radius
r = smaller radius
h = height
l = slant height

Lateral surface area -- 2h (l + b)
Total surface Area -- 2(lb + bh + lh)
Volume -- lbh
Where
l = length
b = breath
h = height
Cube:

Lateral surface area -- 4a*a
Total surface Area -- 6a*a
Volume -- a*a*a
Where
a = length of edge
Right circular cylinder:

Lateral surface area -- 2πrh
Total surface Area -- 2πr(r + h)
Volume -- π*r*r*h
Where
r = radius of base
h = height of the cylinder
Right circular cone:

Lateral surface area -- πr l
Total surface Area -- πr(l + r)
Volume -- (1/3)π*r*r*h
Where
h = height
r = radius
l = slant height
Sphere:

Total surface Area -- 4πr2
Volume -- (4/3)π*r*r*r
Where
r = radius
Hemisphere:

Lateral surface area -- 2πr*r
Total surface Area -- 3πr*r
Volume -- (2/3)π*r*r*r
Where
r = radius
Spherical shell:

Total surface Area -- 4π (R*R – r*r)
Volume -- (4/3)π(R*R*R -r*r*r)
Where
R = outer radius
r = inner radius
Volume of bucket:

Total surface Area -- πr(l + (R-r))
Volume -- (πh/3)(R*R- r*r)
Where
R = larger radius
r = smaller radius
h = height
l = slant height
GMAT/CAT PREPARATION EMAIL COURSE DAY 26
CIRCLES:

Circumference of a Circle = 2 x pi x radius =Pi x diameter
Area of a Circle = pi x r x r
Length of an Arc:
An arc is a piece of the circumference.
If n is the degree measure of the arc's central angle, then the formula is:
Length of an Arc = (n/360)(2 x pi x r)
Area of a Sector:
A sector is a piece of the area of a circle.
If n is the degree measure of the sector's central angle, then the formula is:
Area of a Sector = (n/360)(pi)(r)(r)
Characteristics of Circles:
Circles are closed plane curves with all points on the curve equally distant from a fixed point called the center.
A radius of a circle is a line segment from the center to any point on the circle. All radii of a circle are equal.
A chord is a line segment whose endpoints are on the circle.
A diameter of a circle is a chord that passes through the center of the circle. The diameter of a circle is twice its radius and the longest distance between two points on the circle.
A line passing through two points on a circle is a secant.
The area bounded by the circumference and an angle with vertex at the center of the circle is a sector.
An arc is a portion of a circle, usually measured in degrees.
The entire circle is 360 degrees
A semicircle (half a circle) is 180 degrees
A quarter of a circle is an arc of 90 degrees
A central angle is an angle whose vertex is the center of the circle and whose sides are radii of the circle. A central angle is equal in measure to its arc.
An inscribed angle is an angle whose vertex is on the circle and whose sides are chords of the circle. An inscribed angle is equal in measure to one-half its arc.

Properties of a Circle:
If two chords of a circle are equal, their corresponding arcs have equal measure.
Equal arcs subtend equal angles at the center.
A line from centre and perpendicular to a chord bisects the chord.
Equal chords of a circle are equidistant from the centre.
When two circles touch, their centres and their point of contact are collinear.
If the two circles touch externally, the distance between their centres is equal to sum of their radii.
If the two circles touch internally, the distance between the centres is equal to difference of their radii.
Angle at the centre made by an arc is equal to twice the angle made by the arc at any point on the remaining part of the circumference.
If two chords are equal, the arc containing the chords will also be equal.
There can be one and only one circle that touches three non-collinear points.
The angle inscribed in a semicircle is 90 degrees.

Circumference of a Circle = 2 x pi x radius =Pi x diameter
Area of a Circle = pi x r x r
Length of an Arc:
An arc is a piece of the circumference.
If n is the degree measure of the arc's central angle, then the formula is:
Length of an Arc = (n/360)(2 x pi x r)
Area of a Sector:
A sector is a piece of the area of a circle.
If n is the degree measure of the sector's central angle, then the formula is:
Area of a Sector = (n/360)(pi)(r)(r)
Characteristics of Circles:
Circles are closed plane curves with all points on the curve equally distant from a fixed point called the center.
A radius of a circle is a line segment from the center to any point on the circle. All radii of a circle are equal.
A chord is a line segment whose endpoints are on the circle.
A diameter of a circle is a chord that passes through the center of the circle. The diameter of a circle is twice its radius and the longest distance between two points on the circle.
A line passing through two points on a circle is a secant.
The area bounded by the circumference and an angle with vertex at the center of the circle is a sector.
An arc is a portion of a circle, usually measured in degrees.
The entire circle is 360 degrees
A semicircle (half a circle) is 180 degrees
A quarter of a circle is an arc of 90 degrees
A central angle is an angle whose vertex is the center of the circle and whose sides are radii of the circle. A central angle is equal in measure to its arc.
An inscribed angle is an angle whose vertex is on the circle and whose sides are chords of the circle. An inscribed angle is equal in measure to one-half its arc.

Properties of a Circle:
If two chords of a circle are equal, their corresponding arcs have equal measure.
Equal arcs subtend equal angles at the center.
A line from centre and perpendicular to a chord bisects the chord.
Equal chords of a circle are equidistant from the centre.
When two circles touch, their centres and their point of contact are collinear.
If the two circles touch externally, the distance between their centres is equal to sum of their radii.
If the two circles touch internally, the distance between the centres is equal to difference of their radii.
Angle at the centre made by an arc is equal to twice the angle made by the arc at any point on the remaining part of the circumference.
If two chords are equal, the arc containing the chords will also be equal.
There can be one and only one circle that touches three non-collinear points.
The angle inscribed in a semicircle is 90 degrees.
Thursday, November 19, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 25
3-4-5 Triangle:
If a right triangle's leg-to-leg ratio is 3:4, or if the leg-to-hypotenuse ratio is 3:5 or 4:5, it's a 3-4-5 triangle.
5-12-13 Triangle
If a right triangle's leg-to-leg ratio is 5:12, or if the leg-to-hypotenuse ratio is 5:13 or 12:13, then it's a 5-12-13 triangle.
30-60-90 Triangle
The sides of a 30-60-90 triangle are in a ratio of x : x V 3 : 2x.
45-45-90 Triangle
The sides of a 45-45-90 triangle are in a ratio of x : x : x V 2
Polygon:
A polygon is a plane figure that is bounded by a closed path made of straight line segments. These segments are called its edges or sides, and the points where two edges meet are the polygon's vertices or corners.
convex polygon is a simple polygon whose interior angles are convex.
* Every internal angle is less than 180 degrees.
* Every line segment between two vertices remains inside or on the boundary of the polygon.
Concave polygons:
A concave polygon will always have an interior angle with a measure that is greater than 180 degrees.

Quadrilateral:
A quadrilateral is a polygon with four sides or edges and four vertices or corners:
Convex quadrilaterals - parallelograms:
A parallelogram is a quadrilateral with two sets of parallel sides.
Equivalent conditions are that opposite sides are of equal length.
Opposite angles are equal.
The diagonals bisect each other.
Parallelograms also include the square, rectangle, rhombus and rhomboid.
Convex quadrilaterals - other
Kite: two adjacent sides are of equal length and the other two sides also of equal length.
Trapezium : two opposite sides are parallel.
Cyclic quadrilateral: the four vertices lie on a circumscribed circle.
Rectangle:
Rectangle normally refers to a quadrilateral with four right angles.
Properties:
• All angles are 90 degrees.
• Opposite sides are equal in length.
• Opposite sides are parallel.
• Diagonals are equal in length and bisect each other.
If a rectangle has length l and width w
• it has area A = lw
• perimeter P = 2l + 2w = 2(l + w)
• and each diagonal has length v(l^2+w^2).
Rhombus:
A rhombus or rhomb is a quadrilateral whose four sides all have the same length.
A rhombus is an equilateral quadrilateral.
Every rhombus is a parallelogram, and a rhombus with right angles is a square.
Properties
Every rhombus has two diagonals connecting opposite pairs of vertices and two pairs of parallel sides. Any rhombus has the following two properties:
1. Opposite angles of a rhombus have equal measure.
2. The two diagonals of a rhombus are perpendicular.
The first property implies that every rhombus is a parallelogram. A rhombus therefore has all of the properties of a parallelogram:
opposite sides are parallel.
adjacent angles are supplementary
the two diagonals bisect one another.
Any quadrilateral whose two diagonals are perpendicular is called a kite. Every rhombus is a kite, and any quadrilateral that is both a kite and parallelogram is a rhombus.
Square:
a square is a regular quadrilateral. This means that it has four equal sides and four equal angles (90 degree angles, or right angles).
A square is both a rhombus (equal sides) and a rectangle (equal angles) and therefore has all the properties of both these shapes, namely:
The perimeter of a square whose sides have length s is
P=4s
and the area is
A=s^2
Properties:
* The diagonals of a square bisect each other.
* The diagonals of a square bisect its angles.
* The diagonals of a square are perpendicular.
* Opposite sides of a square are both parallel and equal.
* All four angles of a square are equal. (Each is 360/4 = 90 degrees, so every angle of a square is a right angle.)
* The diagonals of a square are equal.
* If the diagonals of a rhombus are equal, then that rhombus must be a square.
* A square can also be defined as a rectangle with all sides equal, or a rhombus with all angles equal, or a parallelogram with equal diagonals that bisect the angles.
* If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths), then it is a square.
* If a circle is circumscribed around a square, the area of the circle is π / 2 (about 1.57) times the area of the square.
* If a circle is inscribed in the square, the area of the circle is π / 4 (about 0.79) times the area of the square.
* A square has a larger area than any other quadrilateral with the same perimeter.
If a right triangle's leg-to-leg ratio is 3:4, or if the leg-to-hypotenuse ratio is 3:5 or 4:5, it's a 3-4-5 triangle.
5-12-13 Triangle
If a right triangle's leg-to-leg ratio is 5:12, or if the leg-to-hypotenuse ratio is 5:13 or 12:13, then it's a 5-12-13 triangle.
30-60-90 Triangle
The sides of a 30-60-90 triangle are in a ratio of x : x V 3 : 2x.
45-45-90 Triangle
The sides of a 45-45-90 triangle are in a ratio of x : x : x V 2
Polygon:
A polygon is a plane figure that is bounded by a closed path made of straight line segments. These segments are called its edges or sides, and the points where two edges meet are the polygon's vertices or corners.
convex polygon is a simple polygon whose interior angles are convex.
* Every internal angle is less than 180 degrees.
* Every line segment between two vertices remains inside or on the boundary of the polygon.
Concave polygons:
A concave polygon will always have an interior angle with a measure that is greater than 180 degrees.

Quadrilateral:
A quadrilateral is a polygon with four sides or edges and four vertices or corners:
Convex quadrilaterals - parallelograms:
A parallelogram is a quadrilateral with two sets of parallel sides.
Equivalent conditions are that opposite sides are of equal length.
Opposite angles are equal.
The diagonals bisect each other.
Parallelograms also include the square, rectangle, rhombus and rhomboid.
Convex quadrilaterals - other
Kite: two adjacent sides are of equal length and the other two sides also of equal length.
Trapezium : two opposite sides are parallel.
Cyclic quadrilateral: the four vertices lie on a circumscribed circle.
Rectangle:
Rectangle normally refers to a quadrilateral with four right angles.
Properties:
• All angles are 90 degrees.
• Opposite sides are equal in length.
• Opposite sides are parallel.
• Diagonals are equal in length and bisect each other.
If a rectangle has length l and width w
• it has area A = lw
• perimeter P = 2l + 2w = 2(l + w)
• and each diagonal has length v(l^2+w^2).
Rhombus:
A rhombus or rhomb is a quadrilateral whose four sides all have the same length.
A rhombus is an equilateral quadrilateral.
Every rhombus is a parallelogram, and a rhombus with right angles is a square.
Properties
Every rhombus has two diagonals connecting opposite pairs of vertices and two pairs of parallel sides. Any rhombus has the following two properties:
1. Opposite angles of a rhombus have equal measure.
2. The two diagonals of a rhombus are perpendicular.
The first property implies that every rhombus is a parallelogram. A rhombus therefore has all of the properties of a parallelogram:
opposite sides are parallel.
adjacent angles are supplementary
the two diagonals bisect one another.
Any quadrilateral whose two diagonals are perpendicular is called a kite. Every rhombus is a kite, and any quadrilateral that is both a kite and parallelogram is a rhombus.
Square:
a square is a regular quadrilateral. This means that it has four equal sides and four equal angles (90 degree angles, or right angles).
A square is both a rhombus (equal sides) and a rectangle (equal angles) and therefore has all the properties of both these shapes, namely:
The perimeter of a square whose sides have length s is
P=4s
and the area is
A=s^2
Properties:
* The diagonals of a square bisect each other.
* The diagonals of a square bisect its angles.
* The diagonals of a square are perpendicular.
* Opposite sides of a square are both parallel and equal.
* All four angles of a square are equal. (Each is 360/4 = 90 degrees, so every angle of a square is a right angle.)
* The diagonals of a square are equal.
* If the diagonals of a rhombus are equal, then that rhombus must be a square.
* A square can also be defined as a rectangle with all sides equal, or a rhombus with all angles equal, or a parallelogram with equal diagonals that bisect the angles.
* If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths), then it is a square.
* If a circle is circumscribed around a square, the area of the circle is π / 2 (about 1.57) times the area of the square.
* If a circle is inscribed in the square, the area of the circle is π / 4 (about 0.79) times the area of the square.
* A square has a larger area than any other quadrilateral with the same perimeter.
Wednesday, November 18, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 24
Types of triangles:
Equilateral triangle:
All sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°.
Isosceles triangle:
Two sides are equal in length.An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length.
Scalene triangle:
All sides and internal angles are different from one another.
Oblique triangle:
Triangles that do not have an angle that measures 90° are called oblique triangles.

Acute triangle:
A triangle that has all interior angles measuring less than 90° is an acute triangle or acute-angled triangle.
Obtuse triangle:
A triangle that has one angle that measures more than 90° is an obtuse triangle or obtuse-angled triangle.

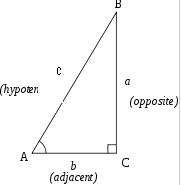
Right triangle:
A right triangle (or right-angled triangle) has one of its interior angles measuring 90° (a right angle).
The side opposite to the right angle is the hypotenuse; it is the longest side in the right triangle.
The other two sides are the legs or catheti of the triangle.
Pythagorean theorem:
The sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse: a2 + b2 = c2, where a and b are the lengths of the legs and c is the length of the hypotenuse.
Equilateral triangle:
All sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°.
Isosceles triangle:
Two sides are equal in length.An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length.
Scalene triangle:
All sides and internal angles are different from one another.
Oblique triangle:
Triangles that do not have an angle that measures 90° are called oblique triangles.

Acute triangle:
A triangle that has all interior angles measuring less than 90° is an acute triangle or acute-angled triangle.
Obtuse triangle:
A triangle that has one angle that measures more than 90° is an obtuse triangle or obtuse-angled triangle.

Right triangle:
A right triangle (or right-angled triangle) has one of its interior angles measuring 90° (a right angle).
The side opposite to the right angle is the hypotenuse; it is the longest side in the right triangle.
The other two sides are the legs or catheti of the triangle.
Pythagorean theorem:
The sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse: a2 + b2 = c2, where a and b are the lengths of the legs and c is the length of the hypotenuse.

Tuesday, November 17, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 23
TRIANGLES
Interior Angles of a Triangle:
The three interior angles of any triangle add up to 180 degrees
Example: In triangle XYZ, angle Y is twice angle X and angle Z is 40 degrees more than angle Y. How many degrees are in the three angles?
The three angles must total 180 degrees.
Let x = angle X, 2x = angle Y, and 2x + 40 = angle Z:
x + 2x + (2x + 40) = 180.
Angle X = 28 degrees Angle Y = 56 degrees Angle Z = 96 degrees
Similar Triangles

Similar triangles have the same shape;
Two triangles are similar if
(i) their corresponding angles are equal, and
(ii) their corresponding sides are proportional
If ΔABC ~ ΔDEF, then by definition
∠A = ∠D, ∠B = ∠E, ∠D = ∠F and AB/DE=BC/EF=CA/FD
AAA similarity-If in two triangles, the corresponding angles are equal the triangles are similar.
SSS similarity-If the corresponding sides of two triangles are proportional the triangles are
similar.
SAS similarity-If one angle of a triangle is equal to one angle of the other triangle and the sides
containing these angles are proportional, the triangles are similar.
Area of Triangle
Area of Triangle = 1/2 (Base) (Height)
The height is the perpendicular distance between the side that is chosen as the base and the opposite vertex.
Triangle Inequality Theorem
The length of one side of a triangle must be greater than the difference and less than the sum of the lengths of the other two sides.
BASIC PROPORTIONALITY THEOREM
If a line is drawn parallel to one side of a triangle, the other two sides of the triangle are divided proportionally.
If a line divides any two sides of a triangle in the same ratio, the line is parallel
to third side of the triangle.
BISECTOR OF AN ANGLE
The internal bisector of an angle of a triangle divides the opposite side in the ratio of sides containing the angle.
IMPORTANT RESULTS
If a perpendicular is drawn from the vertex of the right angle of a right triangle
to the hypotenuse, the triangles on each side of the perpendicular are similar to
each other and to the triangle.
The ratio of the areas of similar triangles is equal to the ratio of the squares on
their corresponding sides.
Interior Angles of a Triangle:
The three interior angles of any triangle add up to 180 degrees
Example: In triangle XYZ, angle Y is twice angle X and angle Z is 40 degrees more than angle Y. How many degrees are in the three angles?
The three angles must total 180 degrees.
Let x = angle X, 2x = angle Y, and 2x + 40 = angle Z:
x + 2x + (2x + 40) = 180.
Angle X = 28 degrees Angle Y = 56 degrees Angle Z = 96 degrees
Similar Triangles

Similar triangles have the same shape;
Two triangles are similar if
(i) their corresponding angles are equal, and
(ii) their corresponding sides are proportional
If ΔABC ~ ΔDEF, then by definition
∠A = ∠D, ∠B = ∠E, ∠D = ∠F and AB/DE=BC/EF=CA/FD
AAA similarity-If in two triangles, the corresponding angles are equal the triangles are similar.
SSS similarity-If the corresponding sides of two triangles are proportional the triangles are
similar.
SAS similarity-If one angle of a triangle is equal to one angle of the other triangle and the sides
containing these angles are proportional, the triangles are similar.
Area of Triangle
Area of Triangle = 1/2 (Base) (Height)
The height is the perpendicular distance between the side that is chosen as the base and the opposite vertex.
Triangle Inequality Theorem
The length of one side of a triangle must be greater than the difference and less than the sum of the lengths of the other two sides.
BASIC PROPORTIONALITY THEOREM
If a line is drawn parallel to one side of a triangle, the other two sides of the triangle are divided proportionally.
If a line divides any two sides of a triangle in the same ratio, the line is parallel
to third side of the triangle.
BISECTOR OF AN ANGLE
The internal bisector of an angle of a triangle divides the opposite side in the ratio of sides containing the angle.
IMPORTANT RESULTS
If a perpendicular is drawn from the vertex of the right angle of a right triangle
to the hypotenuse, the triangles on each side of the perpendicular are similar to
each other and to the triangle.
The ratio of the areas of similar triangles is equal to the ratio of the squares on
their corresponding sides.
Sunday, November 8, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 22
Supplementary Angles:
If the sum of two angles is 180 degrees ie, if they form a straight line , the two angles are supplementary.
Each angle is called the supplement of each other.
Complementary Angles:
If the sum of two angles is 90 degrees.
Reflex Angles:
Angles larger than two right angles but less than a full circle (between 180° and 360°) are called reflex angles.
Acute Angles:
Those angles whose measure is less than 90 degrees
Obtuse Angles:
Those angles whose measure is greater than 90 degrees but less than 180 degrees.
Right Angles:
If two supplementary angles are equal, they are both right angles.
A right angle is half of a straight line and measures exactly 90 degrees.

Intersecting Lines:
When two lines intersect, four angles are formed.
Adjacent angles are supplementary and vertical angles are equal.

Vertical Angles:
Two angles opposite each other, formed by two intersecting straight lines that form an "X"-like shape, are called vertical angles or opposite angles. These angles are equal in measure.
Straight Angles:
Has its sides lying along a straight line and equal to 180 degrees.
Adjacent Angles:
Angles that share a common vertex and edge but do not share any interior points are called adjacent angles.
Parallel Lines and Transversals:
A transversal (line t) across parallel lines form four equal acute angles and four equal obtuse angles.
The top line (line l) is parallel to the bottom line (line m) and line t is the transversal.

Angles 1, 2, 5 and 8 are all equal and acute.
Angles 3, 4, 6 and 7 are all equal and obtuse.
In addition, each of the acute angles is supplementary to each of the obtuse angles. Angles 1 and 4 are supplementary, as are 2 and 3, 2 and 6, and so on.
If the sum of two angles is 180 degrees ie, if they form a straight line , the two angles are supplementary.
Each angle is called the supplement of each other.
Complementary Angles:
If the sum of two angles is 90 degrees.
Reflex Angles:
Angles larger than two right angles but less than a full circle (between 180° and 360°) are called reflex angles.
Acute Angles:
Those angles whose measure is less than 90 degrees
Obtuse Angles:
Those angles whose measure is greater than 90 degrees but less than 180 degrees.
Right Angles:
If two supplementary angles are equal, they are both right angles.
A right angle is half of a straight line and measures exactly 90 degrees.

Intersecting Lines:
When two lines intersect, four angles are formed.
Adjacent angles are supplementary and vertical angles are equal.

Vertical Angles:
Two angles opposite each other, formed by two intersecting straight lines that form an "X"-like shape, are called vertical angles or opposite angles. These angles are equal in measure.
Straight Angles:
Has its sides lying along a straight line and equal to 180 degrees.
Adjacent Angles:
Angles that share a common vertex and edge but do not share any interior points are called adjacent angles.
Parallel Lines and Transversals:
A transversal (line t) across parallel lines form four equal acute angles and four equal obtuse angles.
The top line (line l) is parallel to the bottom line (line m) and line t is the transversal.

Angles 1, 2, 5 and 8 are all equal and acute.
Angles 3, 4, 6 and 7 are all equal and obtuse.
In addition, each of the acute angles is supplementary to each of the obtuse angles. Angles 1 and 4 are supplementary, as are 2 and 3, 2 and 6, and so on.
GMAT/CAT PREPARATION EMAIL COURSE DAY 21
COORDINATE GEOMETRY
Point on a Plane:
Point of Origin is (0,0)
Points in the xy-plane are represented by two numbers called coordinates:
The first number in the pair is the x-coordinate, which is is the horizontal distance of the point from the origin.Points with positive x-coordinates are on the right of the y-axis and Points with negative x-coordinates are on the left of the y-axis.
The second number is the y-coordinate, which is the vertical distance from the origin.Points with positive y- coordinates are above the x-axis. Points with negative y-coordinates are below the x-axis.
A point is represented by (x, y) where x is called the abscissa and y is called the ordinate.
Distance Between Two Points:
To find the distance between points on a graph by using the distance formula:
2 2
Distance = sqrt((x1 -x2) + (y1 - y2) )
Finding the Slope:
Slope = Change in y/Change in x
= Vertical Rise/Horizontal Run
The slope of the line that contains the points A (2, 3) and B (0, -1) is:
(y2 - y1) / (x2 - x1) = (-1 - 3) / (0 - 2) = -4 / -2 = 2
Slope-Intercept Equation:
Equation to Find the Slope:
To find the slope of a line from an equation, put the equation into the slope-intercept form:
y = mx + b
The slope is m and the y-intercept is b.
To find the slope of the equation 4x + 3y = 4, rearrange it:
4x + 3y = 4
3y = -4x + 4
y = -4/3 x + 4/3
The slope is -4/3
Finding an Intercept:
To find the y-intercept, either:
a)Put the equation into y = mx + b (slope-intercept) form and b is the y-intercept
b)Replace x = 0 into the equation and solve for y.
To find the x-intercept, Replace y = 0 into the equation and solve for x.
Point on a Plane:
Point of Origin is (0,0)
Points in the xy-plane are represented by two numbers called coordinates:
The first number in the pair is the x-coordinate, which is is the horizontal distance of the point from the origin.Points with positive x-coordinates are on the right of the y-axis and Points with negative x-coordinates are on the left of the y-axis.
The second number is the y-coordinate, which is the vertical distance from the origin.Points with positive y- coordinates are above the x-axis. Points with negative y-coordinates are below the x-axis.
A point is represented by (x, y) where x is called the abscissa and y is called the ordinate.
Distance Between Two Points:
To find the distance between points on a graph by using the distance formula:
2 2
Distance = sqrt((x1 -x2) + (y1 - y2) )
Finding the Slope:
Slope = Change in y/Change in x
= Vertical Rise/Horizontal Run
The slope of the line that contains the points A (2, 3) and B (0, -1) is:
(y2 - y1) / (x2 - x1) = (-1 - 3) / (0 - 2) = -4 / -2 = 2
Slope-Intercept Equation:
Equation to Find the Slope:
To find the slope of a line from an equation, put the equation into the slope-intercept form:
y = mx + b
The slope is m and the y-intercept is b.
To find the slope of the equation 4x + 3y = 4, rearrange it:
4x + 3y = 4
3y = -4x + 4
y = -4/3 x + 4/3
The slope is -4/3
Finding an Intercept:
To find the y-intercept, either:
a)Put the equation into y = mx + b (slope-intercept) form and b is the y-intercept
b)Replace x = 0 into the equation and solve for y.
To find the x-intercept, Replace y = 0 into the equation and solve for x.
GMAT/CAT PREPARATION EMAIL COURSE DAY 20
AVERAGE, MEDIAN AND MODE
Average or Arithmetic Mean
To find the average of a set of numbers, find the sum and divide by the number of numbers.
Average = Sum of the terms/Number of terms
To find the average of the five numbers 12, 15, 23, 40, and 50, first add them:
12 + 15 + 23 + 40 + 50 = 140.
Then divide the sum by 5: 140 / 5 = 28.
If Average is known to Find the Sum:
Sum = (Average) X (Number of terms)
If the average of ten numbers is 70, then their sum is 10 X 70, or 700.
To Find a Missing Number:
To find a missing number when the average is given , use the sum.
If the average of four numbers is 8, then the sum of those four numbers is 4 X 8, or 32.
Suppose three of the numbers are 4, 7, and 8.
These three numbers add up to 19 .
Which leaves 13 for the fourth number.
Median:
The median of a set of numbers is the value that falls in the middle of the set.
If you have five test scores, and they are 88, 85, 59, 94, and 73, you must first list the scores in increasing or decreasing order: 59,73, 85, 88, 94.The median is the middle number, or 85.
If there is an even number of values in a set (six test scores, for instance), simply take the average of the two middle numbers.
Mode:
The mode of a set of numbers is the value that appears most often.
If your test scores were 89, 56, 68, 88,99, 95, 95, 84, and 95, the mode of the scores would be 95 because it appears more often than any other score.
If there are two most common value in a set, the set has more than one mode.
Standard Deviation
The standard deviation of a statistical population, a data set, or a probability distribution is the square root of its variance.
Standard deviation is a widely used measure of the variability or dispersion. It may be thought of as the average difference of the scores from the mean of distribution, how far they are away from the mean.
A low standard deviation indicates that the data points tend to be very close to the mean, whereas high standard deviation indicates that the data are spread out over a large range of values.
Average or Arithmetic Mean
To find the average of a set of numbers, find the sum and divide by the number of numbers.
Average = Sum of the terms/Number of terms
To find the average of the five numbers 12, 15, 23, 40, and 50, first add them:
12 + 15 + 23 + 40 + 50 = 140.
Then divide the sum by 5: 140 / 5 = 28.
If Average is known to Find the Sum:
Sum = (Average) X (Number of terms)
If the average of ten numbers is 70, then their sum is 10 X 70, or 700.
To Find a Missing Number:
To find a missing number when the average is given , use the sum.
If the average of four numbers is 8, then the sum of those four numbers is 4 X 8, or 32.
Suppose three of the numbers are 4, 7, and 8.
These three numbers add up to 19 .
Which leaves 13 for the fourth number.
Median:
The median of a set of numbers is the value that falls in the middle of the set.
If you have five test scores, and they are 88, 85, 59, 94, and 73, you must first list the scores in increasing or decreasing order: 59,73, 85, 88, 94.The median is the middle number, or 85.
If there is an even number of values in a set (six test scores, for instance), simply take the average of the two middle numbers.
Mode:
The mode of a set of numbers is the value that appears most often.
If your test scores were 89, 56, 68, 88,99, 95, 95, 84, and 95, the mode of the scores would be 95 because it appears more often than any other score.
If there are two most common value in a set, the set has more than one mode.
Standard Deviation
The standard deviation of a statistical population, a data set, or a probability distribution is the square root of its variance.
Standard deviation is a widely used measure of the variability or dispersion. It may be thought of as the average difference of the scores from the mean of distribution, how far they are away from the mean.
A low standard deviation indicates that the data points tend to be very close to the mean, whereas high standard deviation indicates that the data are spread out over a large range of values.
Thursday, November 5, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 19
Group Discussions are common in selection process .People watching your discussion see at your body language, the way you speak, the way you show your presence at the GD, the way you move with other people etc.Here are some of the important do's and dont's in GD
DO's:
Do Have confidence in yourself.
Do think of your GD mates as your friends.
Do get updated with current affairs and general topics.
Do take a pen and paper with you.
Start the discussion if possible because The person who speaks first and last will get additional points.
Do start with greetings if you are the first to speak.
Do Introduce yourself.Just saying your name will be sufficient.
Do speak with optimum volume level that will be sufficient for the other members to hear you.
Do Validate your points with stats. Give proofs/incidents to make your point more effective.
The content of your speech matters.
Do make note of important points that you have in mind and what others say.
Do Look at all the people. Move your heads/eyes towards all the people.
Try to use words like "As my friend said", "As my friend rightly pointed out", "I agree with what he/she said" etc. If you know his/her name, use his/her name.
If the discussion gets centered at the same point, try to bring in new dimension to the discussion with your points.
Keep your points short and simple.
Try to conclude the discussion. During conclusion, list out all the important points that were discussed from you notes.
DONT's:
If you are sure about your points start the discussion else listen to what others so that you can get some idea on the topic.
Don't speak irrelevant to the topic. If the discussion drifts away from the topic, pull it back.
Don't sit quiet for a long time or till all the people finish speaking. Grab your chance as soon as possible.
Don't point on to others with your finger.
Don't speak too loud or too low voice.
Don't leave a pause between two points.
Don't jump from one point to another abruptly.
Don't use negatives like "I don't agree with you", I strongly object" etc instead Use words like "My points differs from your point" .
Don't shake your legs.
Don't cross your fingers.
Keep yourself cool throughout the discussion and be the winner.
DO's:
The content of your speech matters.
DONT's:
GMAT/CAT PREPARATION EMAIL COURSE DAY 18
CALENDAR PROBLEMS
For solving the calendar problems we may need the following info.
We can find the number day on which a particular date falls by finding the number of odd days.
Odd days are obtained by finding the remainder when the no of days are divided by 7
The no of days in each month in a year is Jan-31, Feb-28(29), Mar-31, Apr-30, May-31, Jun-30, Jul-31, Aug-31, Sep-30, Oct-31, Nov-30, Dec-31
No of odd days in each month in a year -Jan-3, Feb-0(1), Mar-3, Apr-2, May-3, Jun-2, Jul-3, Aug-3, Sep-2, Oct-3, Nov-2, Dec-3
Leap year: A year is said to be Leap year if it contains366 days (ie,29 days in February)
How to find whether a year is leap year or not ?
1) We get a leap year if that year is divisible by 4 exactly
2) Years divisible by 100 and not by 400 is not a leap year
1st January 0001 was a Monday.
Calendar repeats after every 400 years.
Calendar moves ahead by number of odd days.
In a normal year 1st January and 2nd July and 1st October fall on the same day.
In a leap year 1st January 1st July and 30th September fall on the same day.
Ordinary year = 52 weeks + 1 odd day
Leap year = 52 weeks + 2 odd day
100 Years = 76 ordinary years +24 leap years
100 years has 5 odd days
400 years has (20+1) odd days ie , 0 odd days.
Here are the steps to find out the number of odd days.
Step 1: Find leap year or not.
Step 2: Find out total odd days on months.
Step 3: Find out the total odd days on year.
Step 4: Finally add the total number of odd days between the given dates.
Jan 1, 2001 is a Monday, depending on odd day, we have
1 is Monday
2 is Tuesday
3 is Wednesday
4 is Thursday
5 is Friday
6 is Saturday
0 or 7 is Sunday
For solving the calendar problems we may need the following info.
How to find whether a year is leap year or not ?
1) We get a leap year if that year is divisible by 4 exactly
2) Years divisible by 100 and not by 400 is not a leap year
100 years has 5 odd days
400 years has (20+1) odd days ie , 0 odd days.
Step 1: Find leap year or not.
Step 2: Find out total odd days on months.
Step 3: Find out the total odd days on year.
Step 4: Finally add the total number of odd days between the given dates.
1 is Monday
2 is Tuesday
3 is Wednesday
4 is Thursday
5 is Friday
6 is Saturday
0 or 7 is Sunday
Tuesday, November 3, 2009
GMAT/CAT PREPARATION EMAIL COURSE DAY 17
CLOCKS:
Clock angle problems relate two different measurements - angles and time.
To answer the problem the relationship between the time and the angle between the hands .
-->A dial of the clock is divided into 60 parts each called minute spaces.
-->The hour hand goes 5 minute spaces in one hour and minutes hand goes 60 minute spaces in one hour.
-->Thus the minute hand covers 6 degress per minute.
-->The hour hand covers 30 degrees per hour.
-->The minute hand gains 55 minute spaces over the hour hand in one hour
-->When two hands are in 90 degree they are 15 minute spaces apart. This occurs twice in an hour.
-->When the two hands are in opposite directions(ie,180 degrees)they are 30 minute hands apart this occurs once in an hour
-->Two hands are in straight line when they coincide or are in opposite directions
-->The angle between the two hands = 6(x-11/12m)
X= hour hand convert into minute spaces i.e.* 5 of the earlier clock
M = the later part of the time i.e. minutes

Clock angle problems relate two different measurements - angles and time.
To answer the problem the relationship between the time and the angle between the hands .
-->A dial of the clock is divided into 60 parts each called minute spaces.
-->The hour hand goes 5 minute spaces in one hour and minutes hand goes 60 minute spaces in one hour.
-->Thus the minute hand covers 6 degress per minute.
-->The hour hand covers 30 degrees per hour.
-->The minute hand gains 55 minute spaces over the hour hand in one hour
-->When two hands are in 90 degree they are 15 minute spaces apart. This occurs twice in an hour.
-->When the two hands are in opposite directions(ie,180 degrees)they are 30 minute hands apart this occurs once in an hour
-->Two hands are in straight line when they coincide or are in opposite directions
-->The angle between the two hands = 6(x-11/12m)
X= hour hand convert into minute spaces i.e.* 5 of the earlier clock
M = the later part of the time i.e. minutes
Subscribe to:
Comments (Atom)

